Let ![]() be any nonempty set. By
be any nonempty set. By ![]() we will denote the power set of
we will denote the power set of ![]() , i.e. the set containing all possible subsets of
, i.e. the set containing all possible subsets of ![]() :
:
![]()
A topology on ![]() is a subset
is a subset ![]() satisfying:
satisfying:
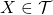 and
and 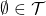 ,
,- If
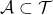 , then
, then 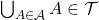 ,
, - If
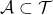 consists of finitely many elements, then
consists of finitely many elements, then 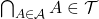 .
.
As usual, a function ![]() , where
, where ![]() and
and ![]() are topological spaces, is continuous if
are topological spaces, is continuous if ![]() for any
for any ![]() . It is easy to check that the composition of continuous functions is continuous.
. It is easy to check that the composition of continuous functions is continuous.
Lemma: If 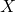 is a non-empty set and
is a non-empty set and 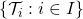 a family of topologies on
a family of topologies on 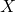 (where
(where 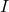 is an arbitrary index set), then
is an arbitrary index set), then
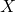 .
.
![]()
Proof: It is straightforward to verify that
Lemma: If 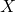 is a non-empty set,
is a non-empty set, 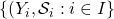 a family of topological spaces (where
a family of topological spaces (where 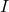 is an arbitrary index set) and for each
is an arbitrary index set) and for each 
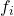 is a function from
is a function from 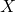 to
to  . Then, there is a minimal (i.e. smallest) topology
. Then, there is a minimal (i.e. smallest) topology 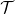 on
on 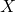 such that each function
such that each function 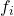 is continuous as a function from
is continuous as a function from 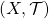 to
to 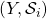 .
.
Proof: Clearly, there exists a topology making each
![]()
The topology in the previous lemma, being defined by ![]() , the topological spaces
, the topological spaces ![]() and the functions
and the functions ![]() (
(![]() ) is called the initial topology.
) is called the initial topology.
Given the family ![]() of topological spaces, we can consider the cartesian product
of topological spaces, we can consider the cartesian product
![]()
![]()
Lemma: Let 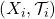 be a collection of topological spaces,
be a collection of topological spaces, 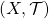 and their product space with product topology. Then, the projection maps
and their product space with product topology. Then, the projection maps 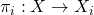 are open, i.e. for
are open, i.e. for 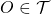 we have
we have 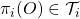 .
.
Proof: Let
Lemma: Let 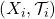 be a collection of topological spaces,
be a collection of topological spaces, 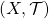 their product space with product topology and
their product space with product topology and  a function. Then,
a function. Then, 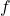 is continuous if and only if
is continuous if and only if 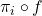 is continuous for every
is continuous for every  . Here,
. Here, 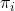 is again the projection
is again the projection 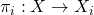 .
.
Proof: Contininuity of
Now, assume that
